Power Law Investing in Crowdfunding

In Venture Capital (VC) and Angel investing, there is a common adage that many investors follow that says to “swing for the fences” versus looking for the safer singles or doubles.

Is there justification for such a strategy, and does equity crowdfund investing warrant a similar approach?

Swinging for the fences is one way of saying you need to be aiming for the big, long-tail returns of power law investing.

Today we will explore why life is not as “normal” as we think, what the power law is, why it is important to early-stage investing, and how to use it in your equity crowdfunding portfolio strategy.

Background – the Normal Distribution

Think of some items that have a measurable characteristic: for example, your height, the weight of your German Shepherd, or the measurements on some plastic parts that you 3D printed.

Assuming large enough sample sizes, if you were to measure and observe these and other physical objects, they would likely follow something called a normal or “Gaussian” distribution. Also known as the bell curve, it is the statistical distribution of a dataset that describes the probability of occurrence for random variables.

A normal distribution has well-defined characteristics that make it convenient for applying to datasets in real life. It has a finite mean (i.e. average) and a finite variance (standard deviation is the square root of variance), which describes how closely-packed the population is distributed about the mean.

In a normal distribution, the two tails drop off towards zero very fast in each direction.

As we will see, however, while the normal distribution is convenient and easy to understand, most of the real world does not follow normal distributions.

The Human Brain Craves “Normal”

“The greatest shortcoming of the human race is our inability to understand the exponential function.” — Albert Allen Bartlett

With much of what is taught in school and statistics, the human brain is conditioned to assume that most datasets we encounter in life are normal distributions. Why is that?

First, there is some truth to this assumption due to the central limit theorem (CLT). The CLT states that for a population with a finite variance (a key assumption we will show does not hold for early-stage investing), for a large enough sample size (typically n>30), the mean of all random samples will approximately equal the mean of the population.

Next, consider our evolutionary history as a species. Many objects and situations that our ancestors encountered in daily life could be approximated as normal distributions for quicker assessment. Many of these things were key to our survival – estimating the potential height and weight of enemy warriors, the size and weight of prey, crop yields, annual rainfall, and other outcomes.

However, as society evolved and more complex social constructs came into existence – such as financial markets, large organizations, and the internet – our world started being driven more by factors that are not best approximated by normal distributions.

Assuming that the entire world is normal when it is not can lead to unexpected and catastrophic events. Consider when major bubbles or busts occur in economics that could not have been possible under our Gaussian models. Or when natural disasters, such as earthquakes and floods, far worse than previously thought possible occur.

Many of these events are better represented by power laws. Similar to the turkey problem in investing, they are completely unexpected or statistically improbable before they occur, but become part of our models after.

Power Law Equation

A power law follows the exponential equation below, where the outcome scales as a function of the exponent alpha:

p(x)=Cx^-α

Where:

• p(x) is the probability of occurrence for a given event (e.g. probability of an investment’s returns “x”)
• C is a constant (a mathematical property adjusted to ensure the area under the curve sums to one), equal to C=(α-1)x_min^(α-1)
• x is the random variable (e.g. a return multiple of a given investment)
• α: “alpha” – the scaling exponent, is a key property of the dataset that we will discuss, which influences how fat the tail is (e.g. dependent on time and growth rate, as discussed below)

The Power Law Equation for Early-Stage Investing

As derived here in a simplified model for Venture Capital, alpha can be represented in terms of time to exit (t) and annual growth rate (g) as:

α = 1/(t*g) + 1

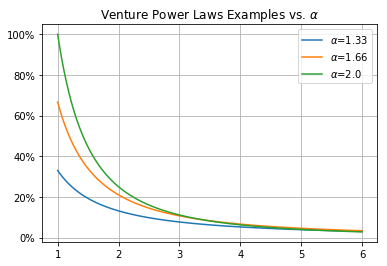
Some values of alpha are below for example investment time horizons and growth rates. Note that the higher the outcome for investor returns – represented by a larger denominator of time and growth rate – the lower the alpha value.

• t=5 years, g=20% → alpha = 2.0
• t=5 years, g=30% → alpha = 1.67
• t=10 years, g=30% → alpha = 1.33

Below is what those sample power law returns would look like. While it is hard to see without zooming in, note that higher growth rates and longer exit times (i.e. larger overall investment outcomes) correspond to a lower alpha, and thus a “fatter” tail.

Zooming in on the tails and including alpha=3, to represent and contrast stock-market like returns:

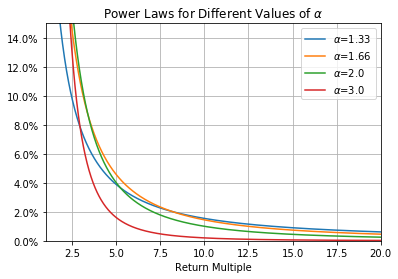
Takeaway: it is advantageous for investors to look for returns that have lower alphas, corresponding to higher probabilities for higher potential returns.

Characteristics of Power Laws

To oversimplify, a power law is a population of independent inputs where smaller outcomes are more likely and larger outcomes are less likely.

It differs from a normal distribution because extremely large outcomes, although rare, are relatively more likely to occur when compared to a normal distribution, and thus can’t be ignored. This is called the effect of the “long tail” or “fat tail”. This concept was also popularized as a black swan event by Nicholas Nassim Taleb.

The Long Tail

The long tail is something that affects many parts of our lives, although most people would never know it.

Besides early-stage investing, the impacts of the long tail can be seen in the stock market, careers, health, world wars, wealth, popularity, and city sizes, just to name a few.

Author Nassim Nicholas Taleb, author of Black Swan and Antifragile, argues that events in the long tail actually drive most of human history. This is counter-intuitive to many people’s beliefs that most events in the world follow a normal distribution and can be predicted or modeled.

That is why understanding power laws and rewiring your brain to think about the long tail is one of the most crucial factors when early-stage investing.

The 80/20 Pareto Principle – the power law at work

Have you heard of the 80/20 rule, also known as the Pareto Principle?

This well-known principle originates from Vilfredo Pareto’s discovery that 80% of the land in Italy was owned by 20% of its people. The 80/20 principle is true of the power law behavior for citizen wealth, and has even become an axiom in many fields ranging from customer sales (i.e. 80% of sales will come from 20% of customers), to personal time management (i.e. 20% of your efforts will result in 80% of the results).

Whether all its practitioners realize it or not, the 80/20 rule is probably the best-known example of the power law at work.

Scale Invariance and Fractals

Another property of power laws is their fractal nature, meaning that you can continue breaking each sub-division down into smaller chunks that follow the same distribution.

In mathematics, this is referred to as scale invariance – a property that can be derived from the power law equation, when scaled by a constant “c”.

This is saying that when scaling the power law equation by a constant “c”, the end result is directly proportional to the original power law. Note: the “∝” symbol here signifies “proportional to” – not to be confused with the alpha discussed elsewhere in this article.

This scaling invariance property has two key implications in investing.

1 – The power law continues at each sub-division of outcomes

Going back to the 80/20 wealth example – in the top 20%, you would find that the top 20% of that population has 80% of that population’s wealth. This means the top .2²=4% of the nation controls .8²=64% of the nation’s total wealth, and on and on it goes (.2³=0.8% of the population accounts for .8³=51.2% of wealth, etc.).

Applying the 80/20 rule to VC investments, this back-of-the-envelope approximation – that roughly 1 in 100 investments would return over half of the entire portfolio – is actually a decent reflection of actual VC investment returns.

This is confirmed by Peter Thiel in Zero to One when he says, “The biggest secret in venture capital is that the best investment in a successful fund equals or outperforms the entire rest of the fund combined.”

Historical VC data confirms that a minority of investments account for the majority of returns.

2 – Initial valuations may not be as important as investors think

Do you think that the initial seed stage investors in Uber were splitting hairs over the business’ valuation? If during its seed round Uber had been valued at $10M or $20M instead of $5.5M, would it have been wise for those initial investors to pass because it was over-valued?

Obviously, that would have been a huge mistake! With the potential of a $120B IPO valuation in 2019, that would be over 21,000X return for seed stage investors, ignoring dilution.

There is no mistaking that getting 50% or 25% as much due to an initial valuation is not as sweet. However, at that order of magnitude return in the thousands, the key is being involved at all vs. getting in at the right price.

Thus, nit-picking over small discrepancies in valuations, especially during early-stages when it is extremely difficult to accurately estimate, is one way that you may exclude potential huge, long-tail winners from your portfolio.

Contrasting Power vs. Normal Distributions

To understand the implications of how a power law differs from a normal distribution, let’s go back to the example of human height, which follows a normal distribution.

The thought experiment of what a power law distribution would mean for human height is best summarized by Prof. Aaron Clauset:

If human heights were assumed to follow a power law distribution, “…we would expect ridiculous facts such as 10,000 individuals being as tall as an adult male giraffe, one individual as tall as the Empire State Building (381 meters), and 180 million diminutive individuals standing a mere 17 cm tall.”

While we know these outcomes are physically impossible due to restrictions of human physiology, for a power law, those extreme results lie within the “long tail”, and cannot be ignored.

In the world of finance, having an investment return 50X, 100X, even 1000X when most investments will return 1-5X (or fail) is what separates the top investors from the average investors.

In addition, two of the characteristics that are key to normal distributions – having a finite mean and a finite variance – cannot be assumed finite in the case of power laws.

Life is far from normal

“[W]e don’t live in a normal world, we live under a power law.” — Peter Thiel

Many outcomes and datasets in the modern world – such as financial market returns, city populations, solar flare intensity, and citizen wealth – are better represented by power law distributions.

The below graph shows how a normal distribution compares with power laws. Note how the tails of the normal distribution drop off quickly, while the power laws maintain a “long tail” as they go further to the right. The thickness of the tail depends on a factor called alpha.

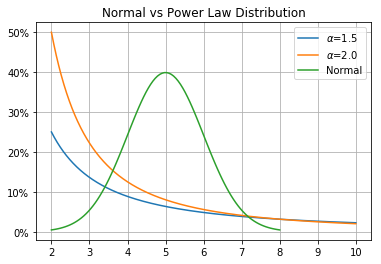
The smaller the alpha, the “fatter” the tail.

As summarized here from various financial returns studies, typical alphas for early-stage Angel and VC investment returns range from roughly 1.70 – 2.27. The so-called cubic law returns of stock markets implies an alpha of roughly 3.0.

Summarizing these alphas:

• Early-stage investing alpha = 1.70-2.27
• Stock market alpha = ~3.0

Thus, while early-stage investing has higher potential risk, the assumption is that this additional risk comes with the benefits of a “fatter” tail, due to lower alpha, and higher potential returns.

Unique Mathematical Properties of Power Laws

The value of alpha drives some important mathematical properties that can influence investment strategies in early-stage investment portfolios.

Power laws of the form x^-α:

1. have an undefined mean and undefined variance when 1<α<2
2. have an undefined mean but a finite variance when 2<α<3
3. have a finite mean and a finite variance for α>3 (required assumption for normal distributions)

When derived from this source code, simulated results for the above three examples look like:

So, what do all these mathematical properties mean for the equity crowdfund investor?

1 – We cannot use a normal distribution to model early-stage returns

From our prior discussion of normal distributions – which required that the data outcomes have a finite variance (meaning α>3) – we CANNOT use normal distributions for early-stage investment modeling, since we have shown alpha is less than 3.

2 – Larger sample sizes (i.e. more investments) leads to increasing mean returns

Further, when alpha is assumed less than 2.0 for early-stage investing, then the mean returns of a portfolio approach infinity as the sample size increases (i.e. you get higher returns as more investments are made).

Have you heard of 500startups? As we will discuss below, there is more to their investment business than just a catchy name.

Applying the Power Law to Early-Stage Investing

“I use two methods to sort through the deluge of startups contacting me. I eliminate the small ideas and weak founders. Then I double down on the great founders and big ideas.” — Jason Calacanis in Angel

To understand some of the most important implications of the power law distribution to early-stage investing, there are three key takeaways from power laws that can help drive your investment strategy.

Power Law lessons applied to investing are:

1. Invest for the long tail: ensure your screening process allows for taking advantage of the “long tail”. In Peter Thiel’s words, “First, only invest in companies that have the potential to return the value of the entire fund. ”
2. Striking out is to be expected: much has been written on the Babe Ruth Effect, which states that “The frequency of correctness does not matter; it is the magnitude of correctness that matters.”
3. Investing in more businesses doesn’t only diversify risk. It can also boost potential returns. As Jerry Neumann notes, “At a given alpha, the more investments you make, the better, because your mean return multiple increases with the number of investments, as does the likeliest highest multiple.” This holds true as long as alpha is less than 2.

Power Law Lesson 1 – Investing in the Long Tail

How do you ensure that you are taking advantage of the long-tail strategy?

Peter Thiel said it best in his book Zero to One – “This implies two very strange rules for VCs. First, only invest in companies that have the potential to return the value of the entire fund. …This leads to rule number two: because rule number one is so restrictive, there can’t be any other rules.”

The key becomes not selecting investments to minimize potential failures, but investing in companies that are at your target alpha with potential for huge returns (i.e. have the ability to return the entire portfolio). Said another way – trying to succeed vs. trying not to fail will result in totally different investment outcomes.

Rewire your brain

• From Normal thinking – “I will invest in solid companies that I reasonably believe have the potential to provide decent returns and have a minimal chance of failing” (no!)
• To Power Law thinking – “I will invest in companies that have massive potential to return more than all my other investments combined” (yes!)

However, this doesn’t come without added risk, which leads us to…

Power Law Lesson 2 – Striking out often is part of the strategy to find the big winners

In his time, Babe Ruth held the record for the most home runs in a season – a record that would stand for 34 years. Do you know what other record Babe Ruth held, until Mickey Mantle would break it 29 years later?

He held the record for the most career strikeouts.

The lesson is this – in pursuit of home runs and big wins, you are going to strike out often.

Does that mean that you swing at every single pitch? Of course not!

You still need to pick your pitches (investments) wisely, but make sure that the ones you do pick have the potential to go out of the park when they succeed, and that you give each one of them your best effort.

To get outsized returns on your investments, you have to invest in deals that others may think are crazy or stupid. Why? Because if everyone knew that a certain business was a sure winner (consensus), then the money would already have poured into that investment and be reflected in its valuation.

As Marc Andreessen said, “Most of the big breakthrough technologies/companies seem crazy at first: PCs, the internet, Bitcoin, Airbnb, Uber, 140 characters. It has to be a radical product. It has to be something where, when people look at it, at first they say, ‘I don’t get it, I don’t understand it. I think it’s too weird, I think it’s too unusual.’”

If your results eventually demonstrate that your screening process is capable of achieving the improbable big winners, then the early failures are all just part of the process. The key is staying alive long enough to have those big winners payout by determining how much to invest in each deal and pacing your investments.

Rewire your brain

• From Normal thinking – “I will screen companies and invest in those that have the lowest likelihood of failure” (no!)
• To Power Law thinking – “I will screen and invest in companies that have massive potential, realizing that failures are part of the process” (yes!)

Power Law Lesson 3 – A Larger Portfolio can Mean Larger Gains

Dave McClure from 500Startups believes “Most VC funds are far too concentrated in a small number (<20–40) of companies. The industry would be better served by doubling or tripling the average # of investments in a portfolio, particularly for early-stage investors where startup attrition is even greater. If unicorns happen only 1–2% of the time, it logically follows that portfolio size should include a minimum of 50–100+ companies in order to have a reasonable shot at capturing these elusive and mythical creatures.”

This is saying that there is a minimum portfolio size so as to have a decent shot of capturing a unicorn within your portfolio.

Remember the unique property of power laws with alpha less than 2? The mean returns approach infinity as additional selections are made. Essentially, the more investments at a given alpha, the better your returns.

This was counter-intuitive when I was starting out, especially because I invested previously in debt vehicles, such as peer-to-peer lending notes on LendingClub and Prosper. In debt-based investments, you have an estimated default rate at each risk level, and so it is well-understood that the more notes you invest in, the less chance you will have of doing worse (or better) than average, and the more you will approach the mean expected return.

This is an example of the normal distribution at work. For those types of investments, normal is good, as we wanted to reduce our deviation from the mean. So we made additional investments to become more confident of a given return.

Power law investing is the opposite. The more you invest, the more likely you will achieve higher returns, instead of converging on a finite expected value.

Rewire your brain

• From Normal thinking – “I will invest in a large enough sample size such that I can be confident that I will return the expected mean” (no!)
• To Power Law thinking – “the more investments I make (at a given alpha), the higher my expected returns” (yes!)

Exception to Rule 3 – Quantity does NOT make up for Quality

Investing in more deals may sound enticing, but the key is to invest in more deals at your given alpha. This is not the same thing as going out and investing in every single deal that gets posted to an equity crowdfunding portal.

It is imperative to remember that you cannot make up for low quality deals by simply investing in more deals. Quantity does not make up for quality.

As you develop your screening and due diligence process, it is likely that your time will be the limiting factor in terms of how many investments you can screen and invest in at your desired level of quality.

Will Equity Crowdfunding Returns Follow the Power Law?

The best Angels and VCs today have an understanding of power law investing and apply these principles to their investments.

A key question that we will need to monitor as US equity crowdfunding matures is: will US equity crowdfunding returns follow the power law?

First, many investors believe that power laws are not the only key to succeeding in venture investing. But even those opposing the view of pure power-law investing strategy acknowledge that power law returns are a portion of their portfolio.

Next, there are many factors where equity crowdfunding will differ from VC and Angel Investing that could influence potential returns. Differences in deal terms and rights, in the types of companies that decide to raise via Reg CF, and other factors will still have to be assessed.

Ultimately, looking at the equity crowdfunding returns in several years will provide insight into the value of alpha for these investments.

So, what do we do until then? How do we decide whether equity crowdfunding is worthy of our hard-earned investment dollars if we have to wait several years to start seeing returns?

In upcoming posts, we will investigate in more detail the types of returns that may be expected. We will look at not only historic Angel and VC returns, but also analyze equity crowdfunding markets in other countries – like the UK and Sweden – that have been operating several years longer than US equity crowdfunding.

In the meantime, Warren Buffett sums up the risk vs. reward trade-off brilliantly:

“If significant risk exists in a single transaction, overall risk should be reduced by making that purchase one of many mutually-independent commitments…Most venture capitalists employ this strategy. Should you choose to pursue this course, you should adopt the outlook of the casino that owns a roulette wheel, which will want to see lots of action because it is favored by probabilities, but will refuse to accept a single, huge bet.”

Take it from one of the best investors ever – don’t make a single, huge bet, no matter how confident you may feel. Know the numbers and stick to your investment strategy, and over the long term, you should reap the rewards of your process.